This post talks about a key factor to CUDA kernel performace: accessing data in the globle memory.

CUDA applications tend to process a massive amount of data from the global memory within a short period of time.

Tiling techniques are engineered that utilize shared memories to reduce the total amount of data that must be acessed from the global memory (read about tiling techniques here The CUDA Parallel Programming Model - 6.Tiling).

In this post I’d like to introduce memory coalescing techniques that can more effectively move data from the global memory into shared memories and registers.

Memory coalescing techniques are often used in conjunction with tiling techniques to allow CUDA devices to reach their performance potential by more efficiently utilizing the global memory bandwidth.

Global Memory Bandwidth

The global memory of a CUDA device is implemented with DRAMs.

DRAM is slow

Data bits are stored in DRAM cells that are small capacitors, where the presence or absence of a tiny amount of electrical charge distinguishes between 0 and 1.

Reading data from a DRAM cell requires the small capacitor to use its tiny electrical charge to drive a highly capacitive line leading to a sensor and set off its detection mechanism that determines whether a sufficient amount of charge is present in the capacitor to qualify as a “1”. This process takes 10 s of nanoseconds in modern DRAM chips. This is in sharp contrast with the sub-nanosecond clock cycle time of modern computing devices.

parallelism and memory access throughput

Because this is a very slow process relative to the desired data access speed (sub-nanosecond access per byte), modern DRAMs use parallelism to increase their rate of data access, commonly referred to as memory access throughput.

DRAM bursts

Each time a DRAM location is accessed, a range of consecutive locations that includes the requested location are actually accessed.

Many sensors are provided in each DRAM chip and they work in parallel, each senses the content of a bit within these consecutive locations.

Once detected by the sensors, the data from all these consecutive locations can be transferred at very high-speed to the processor. These consecutive locations accessed and delivered are referred to as DRAM bursts.

motivation

If an application makes focused use of data from these bursts, the DRAMs can supply the data at a much higher rate than if a truly random sequence of locations were accessed.

Memory Coalescing

Current CUDA devices employ a technique that allows the programmers to achieve high global memory access efficiency by organizing memory accesses of threads into favorable patterns.

how?

• This technique takes advantage of the fact that threads in a warp execute the same instruction at any given point in time.
• The most favorable access pattern is achieved when all threads in a warp access consecutive global memory locations.
• When all threads in a warp execute a load instruction, the hardware detects whether they access consecutive global memory locations. If that’s the case, the hardware combines (coalesces) all these accesses into a consolidated access to consecutive DRAM locations.
• For example, for a given load instruction of a warp, if thread 0 accesses global memory location N2, thread 1 location N+1, thread 2 location N+2, and so on, all these accesses will be coalesced into a single request for consecutive locations when accessing the DRAMs.
• Such coalesced access allows the DRAMs to deliver data as a burst.

matrix multiplication example

Recall from The CUDA Parallel Programming Model - 2. Warps that multidimensional array elements in CUDA are placed into the linearized addressed memory space according to the row-major convention.

Say we have a kernel that computes M x N, where both M and N are 2D row-major array.

Each thread accesses a row of the M array (matrix A below) and a column of the N array (matrix B below).

IMPORTANT: hope this helps with understanding the patterns below

Coalesce happens amongst threads, not amongst different iterations of the loop within each thread’s execution.

You might be thinking: for matrix M in the example below, each thread will read the whole row within its for-loop. But it’s not how the coalesce hardware works here.

Because:

• if you look across the threads in matrix M, they don’t share row accesses at all.
• whereas for matrix N, each thread at iteration 0 combined will access the entire row 0.

Since all threads within a warp executes the same instruction, they all execute the same iteration in the loop at any time. So it doesn’t matter if a thread reads through an entire row during its lifetime. What matters is that all the threads of a warp can be coalesced during each (collected) memory access.

patterns

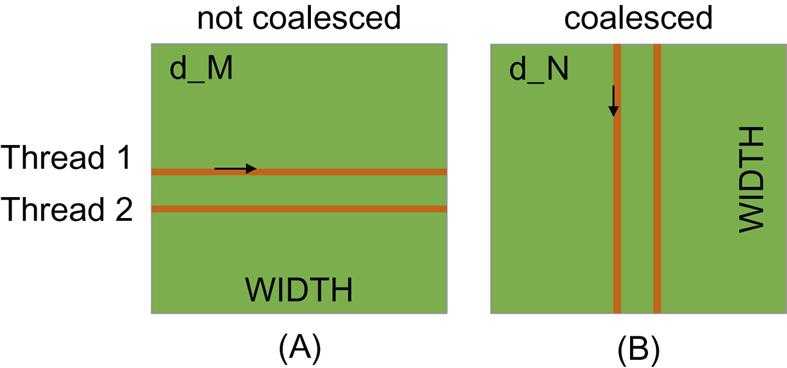
M: unfavorable data access pattern

• fig.(A) above illustrates the data access pattern of the M array
• threads in a warp read adjacent rows
• during iteration 0, threads in a warp read element 0 of rows 0 through 31.
• during iteration 1, these same threads read element 1 of rows 0 through 31.
• None of the accesses will be coalesced.

N: favorable data access pattern

• fig.(B) above illustrates the data access pattern of the N array
• each thread reads a column of N.
• during iteration 0, threads in warp 0 read element 1 of columns 0 through 31.
• all these accesses will be coalesced.

If the above doesn’t make sense to you 🧐, read the post on the matrix application kernel here: CUDA Programming Examples - 1. Matrix Multiplication

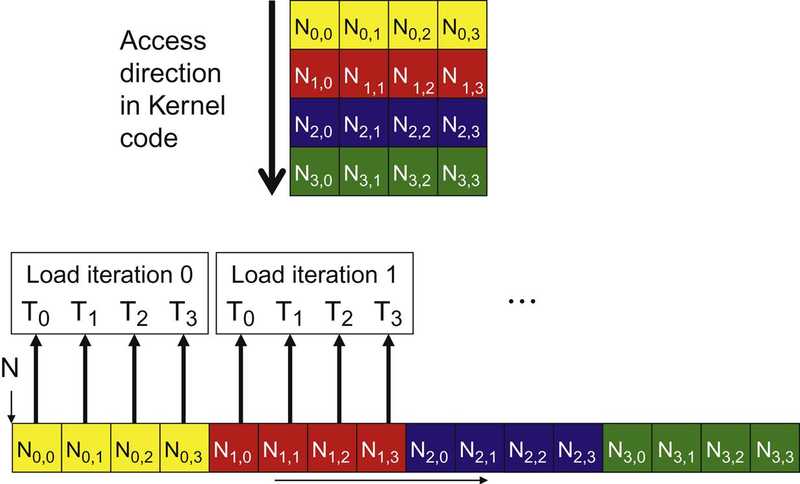
a coalesced access pattern — example of N

• The arrow in the top portion of the figure shows the access pattern of the kernel code.

Recall the for-loop in the kernel:

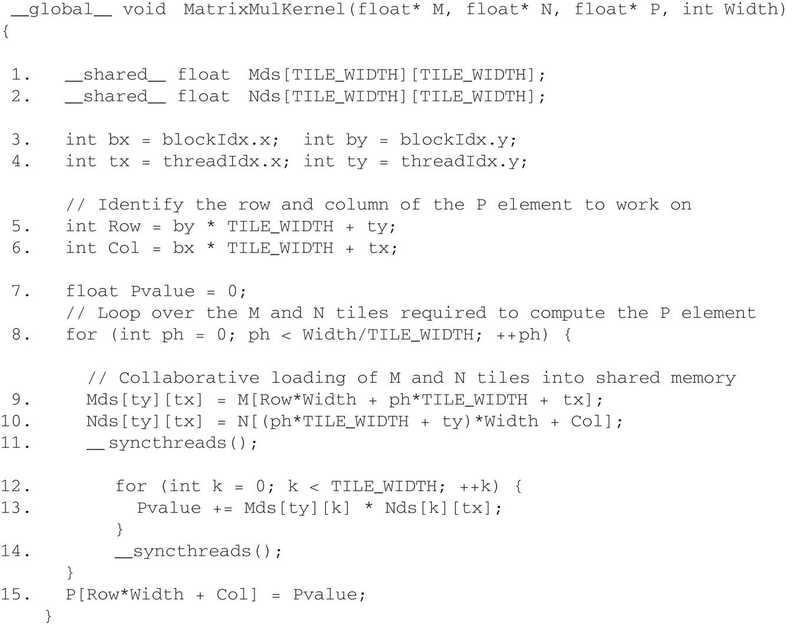
__global__ void MatrixMulKernel (float* M, float* N, float* P, int Width){
    // calculate the row index of the P element and M
    int Row = blockIdx.y * blockDim.y + threadIdx.y;
    // calculate the col index of the P element and N
    int Col = blockIdx.x * blockDim.x + threadIdx.x;

    if((Row < Width) && (Col < Width)){
        float Pvalue = 0;
        //each thread computes one element of the block sub-matrix
        for(int k = 0; k < Width; k++) {
            Pvalue += M[Row*Width + k] * N[k*Width + Col];
        }
        P[Row * Width + Col] = Pvalue;
    }
}

• Within a given iteration of the k loop, the k*Width value is the same across all threads. Recall that Col=blockIdx.x*blockDim.x+threadIdx.x.
• Since the value of blockIndx.x and blockDim.x are of the same value for all threads in the same block, the only part of k*Width+Col that varies across a thread block is threadIdx.x.
• Since adjacent threads have consecutive threadIdx.x values, their accessed elements will have consecutive addresses.

In the pictured example, we are using only 1 block to calculate the entire P matrix, where:

• block size: 4 * 4
• warp size: 4
• Width = 4
• blockDim.x = 4
• blockIdx.x = 0

• In iteration 0, the k value is 0. The index used by each thread for accessing N is

  N[k * Width + Col] = N [k * Width + blockIdx.x * blockDim.x + threadIdx.x]
                   =N[0 * 4 + 0 * 4 + threadidx.x]
                   =N[threadIdx.x]

  That is, within this thread block, the index for accessing N is simply the value of threadIdx.x. The N elements accessed by T0undefined T1undefined T2undefined T3 are N[0]undefined N[1]undefined N[2]undefined and N[3]. This is illustrated with the “Load iteration 0” box of the above figure.

  These elements are in consecutive locations in the global memory. The hardware detects that these accesses are made by threads in a warp and to consecutive locations in the global memory. It coalesces these accesses into a consolidated access. This allows the DRAMs to supply data at a high rate.

• In iteration 1, similarly:

  N[k * Width + Col] = N[k * Width + blockIdx.x * blockDim.x + threadIdx.x]
                   = N[1 * 4 + 0 * 4 + threadidx.x]
                   = N[4 + threadIdx.x]

  The N elements accessed by T0undefined T1undefined T2undefined T3 in this iteration are N[5]undefined N[6]undefined N[7]undefined and N[8], as shown with the “Load iteration 1” box.

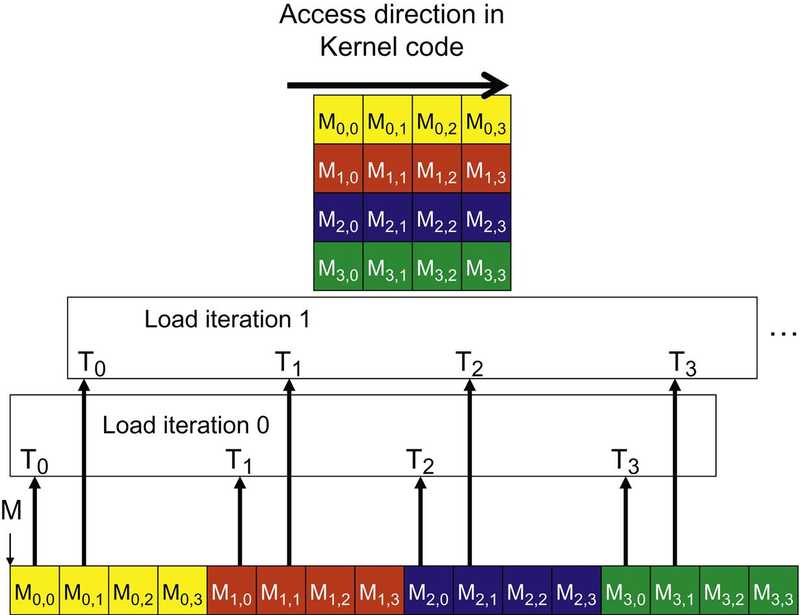
an un-coalesced access pattern — example of M

• The arrow in the top portion of the figure shows that the kernel code for each thread accesses elements of a row in sequence
• block size: 4 * 4
• warp size: 4
• Width = 4
• blockDim.y = 4
• blockIdx.y = 0

• The index used by each thread for accessing M is:

  M[Row * Width + k]  =M[(blockIdx.y * blockDim.y + threadIdx.y) * Width + k]
  
                    =M[((0 * 4+  threadIdx.y) * 4 + 0]
  
                    =M[threadIdx.x * 4]

• The M elements accessed by T0undefined T1undefined T2undefined T3 are M[0]undefined M[4]undefined M[8]undefined and M[12], as shown with the “Load iteration 0” box in the above figure. These elements are not in consecutive locations in the global memory. The hardware cannot coalesce these accesses into a consolidated access.

note on alignment

When accessing words of size 1, 2, 4, 8, or 16 bytes and are aligned, compiler translates this to 1 global memory instruction.

But if size and alignment requirements are not met, compiler would translate it to multiple global memory access instructions.

You can enforce the compiler to align using __align(x)__, for example: struct __align(16)__{...};

Corner Turning

What if we have to iterate through data along the row direction?

• We can use the shared memory to enable memory coalescing — this is the technique called corner turning

how?

• Use a tiled algorithm
• Threads of a block can first cooperatively load the tiles into the shared memory
• Care must be taken to ensure that these tiles are loaded in a coalesced pattern
• Once the data is in shared memory, they can be accessed either on a row basis or a column basis with much less performance variation because the shared memories are implemented as intrinsically high-speed on-chip memory that does not require coalescing to achieve high data access rate.
• A tiled matrix multiplication kernel is shown below: