CUDA Programming - 1. Matrix Multiplication
Notation
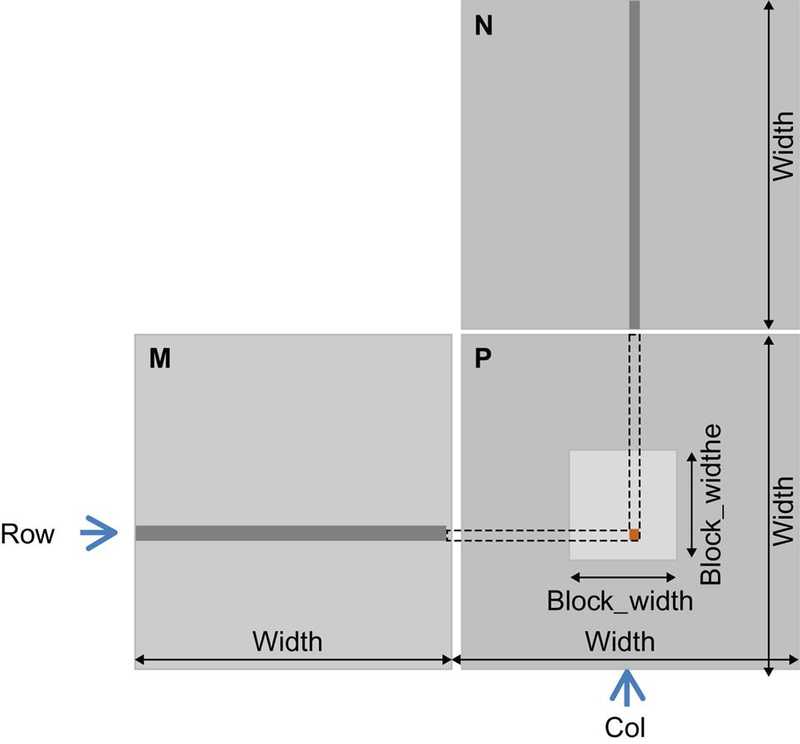
- Matrix
M - Matrix
N - Output Matrix
P - row counter:
i - column counter:
j P(Rowundefined Col)is the element atRow-thposition in the vertical direction andCol-thposition in the horizontal direction
As shown in the picture below, P(RowundefinedCol) (the small square in P) is the inner product of:
- the
Row-throw of M - the
Col-thcolumn of N
Indexing
The row index for the P element is:
Row = blockIdx.y * blockDim.y + threadIdx.y
The column index for the P element is:
Col = blockIdx.x * blockDim.x + threadIdx.x
With this one-to-one mapping, the Row and Col thread indexes are also the row and column indexes for output array
Simple Kernel Using One Thread
Note that the Width used below is the Width in the picture above.
__global__ void MatrixMulKernel (float* M, float* N, float* P, int Width){
// calculate the row index of the P element and M
int Row = blockIdx.y * blockDim.y + threadIdx.y;
// calculate the col index of the P element and N
int Col = blockIdx.x * blockDim.x + threadIdx.x;
if((Row < Width) && (Col < Width>)){
float Pvalue = 0;
//each thread computes one element of the block sub-matrix
for(int k = 0; k < Width; k++) {
Pvalue += M[Row*Width + k] * N[k*Width + Col];
}
P[Row * Width + Col] = Pvalue;
}
}memory access of the for loop
In every iteration of the loop, two global memory accesses are performed for one floating-point multiplication and one floating-point addition.
memory accesses
- One global memory access fetches an M element
- the other fetches an N element
computation performed
- One floating-point operation multiplies the M and N elements fetched
- the other accumulates the product into Pvalue
compute-to-global-memory-access ratio
The compute-to-global-memory-access ratio of the loop is 1.0.
This ratio will likely result in less than 2% utilization of the peak execution speed of the modern GPUs.
We need to increase the ratio by at least an order of magnitude for the computation throughput of modern devices to achieve good utilization.
Execution of the Matrix Multiplication Kernel Within A Block
setting
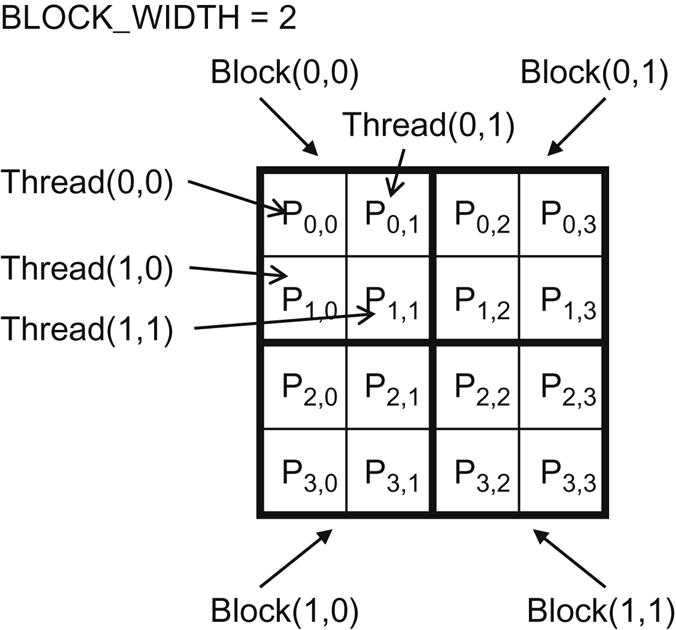
- size of
Pis 4×4 BLOCK_WIDTH = 2
map threads to P
With:
- blocks that are 2×2 arrays of threads
- each thread calculating one P element
The P matrix is now divided into four tiles, and each block calculates one tile.
- In the example,
thread(0undefined0)ofblock(0undefined0)calculatesP(0undefined0) thread(0undefined0)ofblock(1undefined0)calculatesP(2undefined0)
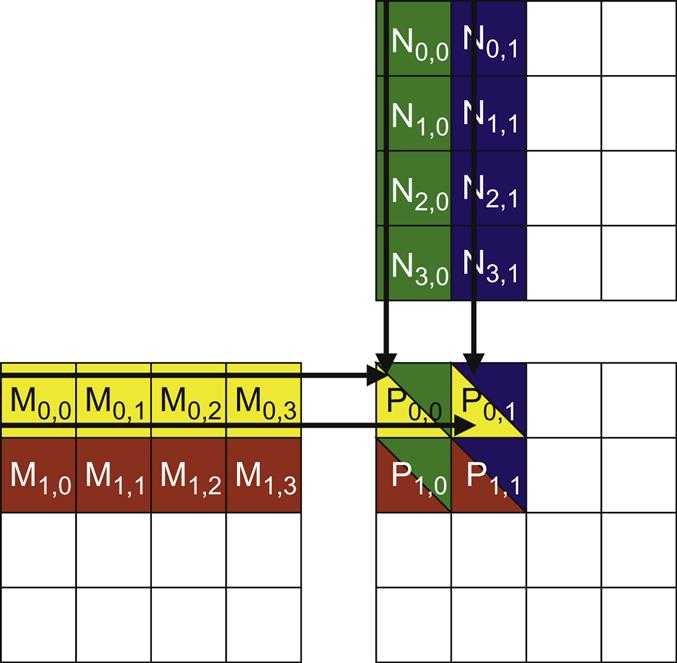
actions of one thread block
The picture below illustrates the multiplication operations in each thread block.
Threads in block (0,0) produce four dot products.
the execution of the for-loop
Use thread(0undefined0) in block(0undefined0) as an example.
-
During the 0th iteration (k=0):
Row * Width + k = 0*4+0 = 0k * Width + Col= 0*4+0 = 0- Therefore, we are accessing
M[0]andN[0], which are the 1D equivalent ofM(0undefined0)andN(0undefined0)
-
During the 1st iteration (k=1):
Row * Width + k = 0*4+1 = 1k * Width + Col = 1*4+0 = 4- We are accessing
M[1]andN[4], which are the 1D equivalent ofM(0undefined1)andN(1undefined0)
Tiled Kernel
To see how to use tiling (corner turning) technique to overcome the fact that row-wise access of matrix M cannot be coalesced, see Corner Turning section in The CUDA Parallel Programming Model - 5.Memory Coalescing.